Flow Coefficient of Butterfly Valve: Cv Value
C v Value when valve in different opening angle
Note:
Cv = Q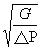 
Q --- Fluid Volume that pass the valve per minute (US gal/min)
P --- Pressure Difference between import and export of the valve (psi)
G --- Density of Fluid.
With the above expressions， You may calculate the flow volume that pass the a valve or pressure loss between the two end of a valve.
Example 1: A 6" butterfly valve is at 70° opening， and a kind of fluid， which density is 0.8， pass the valve with volume 1200 US gal/min， then the pressure loss between the two end is
P = GQ^2 / Cv^2 = 0.8*1200^2 / 958^2 △P = GQ^2 / Cv^2 = 0.8*1200^2/958^2
△P = 1.26 (psi)
Example 2: 10" butterfly valve is at 90° opening， and there is a pressure loss 0.6 psi between
the two end of the valve when a kind of fluid， which density is 0.8， pass the valve，then
the flow volume that pass the valve is
Q = Cv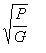 
= 5340 x 
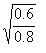= 5340 x 0.866 = 4624.6 (US gal)
Cv Valve is closely related with disc structure. Two regular type of disc are listed as below for reference when selecting Cv Value.
Fig. 1 Split Shaft Design Fig. 2 Tapped Pin Design & Throughout Shaft Pinless Design
Cv Value for Split Shaft I Stem Design (Fig. 1)
|
inch
|
mm
|
10°
|
20°
|
30°
|
40°
|
50°
|
60°
|
70°
|
80°
|
90°
|
|
1 1/2
|
40
|
0.1
|
3
|
6
|
14
|
20
|
38
|
53
|
62
|
73
|
|
2
|
50
|
0.2
|
5
|
9
|
17
|
27
|
53
|
70
|
115
|
145
|
|
21/2
|
65
|
0.4
|
8
|
15
|
26
|
42
|
83
|
105
|
175
|
225
|
|
3
|
80
|
0.6
|
12
|
22
|
38
|
63
|
125
|
160
|
260
|
325
|
|
4
|
100
|
0.8
|
17
|
42
|
73
|
120
|
235
|
305
|
510
|
590
|
|
5
|
125
|
2
|
45
|
88
|
155
|
250
|
490
|
625
|
1000
|
1125
|
|
6
|
150
|
3
|
89
|
145
|
250
|
410
|
800
|
1030
|
1650
|
1950
|
|
8
|
200
|
4
|
148
|
250
|
420
|
700
|
1300
|
1750
|
2725
|
3250
|
|
10
|
250
|
5
|
232
|
390
|
670
|
1150
|
2150
|
2750
|
4300
|
5000
|
|
12
|
300
|
6
|
342
|
550
|
1000
|
1600
|
3100
|
4050
|
5000
|
7500
|
Cv Value for Tapped Pin Design & Throughout Shaft I Stem Pinless Design (Fig.2)
|
inch
|
mm
|
10°
|
20°
|
30°
|
40°
|
50°
|
60°
|
70°
|
80°
|
90°
|
|
1 1/2
|
40
|
0.06
|
3
|
7
|
14
|
25
|
36
|
51
|
70
|
76
|
|
2
|
50
|
0.1
|
5
|
12
|
24
|
45
|
64
|
90
|
125
|
135
|
|
21/2
|
65
|
0.2
|
8
|
20
|
37
|
65
|
98
|
144
|
204
|
220
|
|
3
|
80
|
0.3
|
12
|
22
|
39
|
70
|
116
|
183
|
275
|
302
|
|
4
|
100
|
0.5
|
17
|
36
|
78
|
139
|
230
|
364
|
546
|
600
|
|
5
|
125
|
0.8
|
29
|
61
|
133
|
237
|
392
|
620
|
930
|
1022
|
|
6
|
150
|
2
|
45
|
95
|
205
|
366
|
605
|
958
|
1437
|
1579
|
|
8
|
200
|
3
|
89
|
188
|
408
|
727
|
1202
|
1903
|
2854
|
3136
|
|
10
|
250
|
4
|
151
|
320
|
694
|
1237
|
2047
|
3240
|
4859
|
5340
|
|
12
|
300
|
5
|
234
|
495
|
1072
|
1911
|
3162
|
5005
|
7507
|
8250
|
|
14
|
350
|
6
|
338
|
715
|
1549
|
2761
|
4568
|
7230
|
10844
|
11917
|
|
16
|
400
|
8
|
464
|
983
|
2130
|
3797
|
6282
|
9942
|
14913
|
16388
|
|
18
|
450
|
11
|
615
|
1302
|
2822
|
5028
|
8320
|
13168
|
19752
|
21705
|
|
20
|
500
|
14
|
791
|
1674
|
3628
|
6465
|
10698
|
16931
|
25396
|
27908
|
|
22
|
550
|
17
|
965
|
2042
|
4426
|
7887
|
13052
|
20655
|
30983
|
34048
|
|
24
|
600
|
22
|
1222
|
2587
|
5605
|
9989
|
16528
|
26157
|
39236
|
43116
|
|
26
|
650
|
26
|
1434
|
3036
|
6578
|
11723
|
19397
|
29263
|
46047
|
50600
|
|
28
|
700
|
30
|
1663
|
3522
|
7630
|
12599
|
20036
|
30482
|
46899
|
58696
|
|
30
|
750
|
35
|
1912
|
4050
|
8142
|
13152
|
20411
|
31226
|
47562
|
63328
|
|
32
|
800
|
45
|
2387
|
4791
|
8736
|
13788
|
20613
|
31395
|
48117
|
68250
|
|
34
|
850
|
51
|
2697
|
5414
|
9872
|
15580
|
23293
|
35476
|
54372
|
77123
|
|
36
|
900
|
60
|
3021
|
6063
|
11055
|
17449
|
26086
|
39731
|
60895
|
86375
|
|
40
|
1000
|
84
|
4183
|
8395
|
15307
|
24159
|
36166
|
55084
|
84425
|
119750
|
|
42
|
1050
|
93
|
4601
|
9235
|
16838
|
26575
|
39783
|
60592
|
92868
|
131725
|
|
48
|
1200
|
121
|
5981
|
12001
|
21890
|
34548
|
51718
|
78770
|
120728
|
171243
|